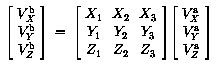
Различные физические процессы проще описываются и расчитываются в своей подходящей координатной системе. Сиситемы координат и Переход к другой
координатной системе описан в работах
Smart (1944), Mead (1970), Goldstein
(1950), Olson (1970) aи в Magnetic and Electric Fields Branch, GSFC(1970).
Russell (1971), Hapgood (1991),Space
Plasma Group website at Ral
Координатные системы, представленные ниже все - геоцентрические. Т.е. начало координат - в центре Земли.
Координатная системя задается направлением одной из осей и напревлением другой оси в плоскости, нормальной к первой. Третья ось фвтоматически дополняет ортогональную систему правой руки.
Переход от системы а к системе b выполняется с помощью матричных преобразований. Для каждого перехода есть матрица T так что Qb = TQa, где Qa - вектор первой координатной системы и Qb - тот же вектор во второй системе. Трансформация полностью задается компонентами матрицы T.
Удобное свойство для обратного перехода состоит в том, что обратная матрица получается из первой простым преобразованием т.е. если :
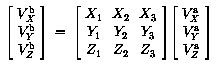
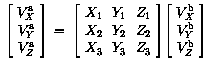
В ряде координатных систем, в частности в GEO и MAG, положение часто определяется через кошироту theta, долготу phi и радиальное расстояние r. Их связь с Картезианскими компонентами:
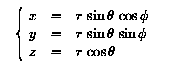
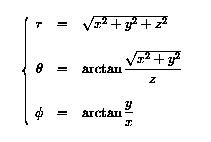
В системе Geocentric Equatorial Inertial Systam (GEI) ось X фиксирована в направлении на Солнце в момент весеннего равноденствия (the first point of Aries (i.e. the position of the sun at the vernal equinox). Это направление есть пересечение плоскостей земного экватора и Эклиптики. Ось Z параллельна оси вращения Земли и Y дополняет ортагональную систему правой руки (Y = Z x X).
Система GEI медленно меняется с изменением направления оси вращения Земли и прецессией Hapgood (1995) описывает, как это учесть.
Система Geographic Coordinate system (GEO) задана осью X ,проходящей через Гринвичский меридиан в плоскости экватора (0° долготы). Она вращается с Землей. Ось Z парралельна оси вращения Земли.
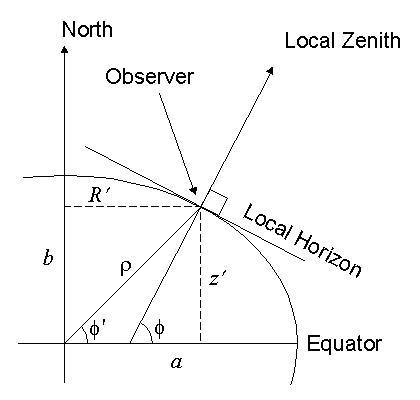
Геодезические координаты определяют положение в терминах широты, долготы и высоты над эллипсоидной поверхностью Земли (рис 1). Подробности для желающих ниже на английским.
|
| Figure 1. Cross section of ellipsoid (taken from Kelso) |
The ellipsoidal surface is a surface of resolution obtained by rotating an ellips around the minor axis. Thus, the geodetic longitude is the same as the geographic longitude, and only a meridional section must be considered.
The local horizon is defined as the plane that is tangent to the Earth's surface at a given position. The surface considered is the reference ellipsoid. The local zenith is the direction away from the point on the Earth's surface perpendicular to the local horizon. On a sphere, this direction is always directly away from the Earth's centre, but on an ellipsoid, this is not the case (except on the equator and at the poles).
The geodetic latitude, phi is the angle between the local zenith and the equatorial plane. Except at the poles and the equator, phi differs from the geocentric latitude phi'.
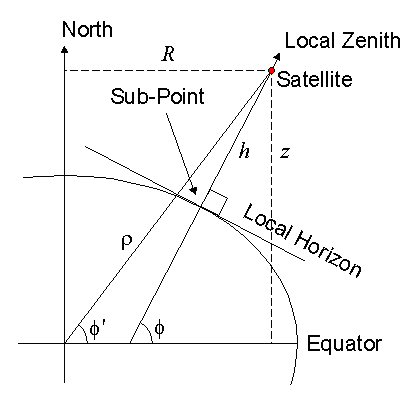
The point on the Earth surface directly below a given point above the surface is not on a line joining the given point and the centre of the Earth. It is the point where the local zenith points to the given point (see Figure 2). The geodetic altitude h is the distance from the point to the surface along the local zenith direction.
|
| Figure 2. Sub-point and altitude (taken from Kelso) |
The reference ellipsoid is defined by two parameters, a, the
semi-major axis, and f, the flattening, defined as:
Global ellipsoidal parameters are derived from satellite data. Historically, local, regional and global best fitting ellipsoids have been considered. Table 1 lists some of these reference ellipsoids.
| Name | semi-major axis [m] |
1/flattening | Application |
|---|---|---|---|
| WGS 84 | 6378137 | 298.257 | DoD (GPS) |
| GRS 80 | 6378137 | 298.257 | IAG (Geo Ref Sys) |
| WGS 72 | 6378135 | 298.26 | DoD (Doppler) |
| GRS 67 | 6378160 | 298.25 | Australia 1966, South America 1969 |
| IAU (1964) | 6378160 | 298.25 | |
| Krassovsky (1940) | 6378245 | 298.3 | Russia |
| International (1924) | 6378388 | 297 | Europe (ReTrig) |
| Clarke (1880) | 6378249 | 293 | France, Africa |
| Clarke (1866) | 6378206 | 294.98 | North America |
| Bessel (1841) | 6377397 | 299.15 | German DHDN |
| Airy (1830) | 6376542 | 299 | Great Britain |
| Everest (1830) | 6377276 | 300 | India |
The implementations in SPENVIS and UNILIB use the IAU (1964) reference ellipsoid.
The conversion from ellipsoidal coordinates to cartesian coordinates is given by:
| X | = | (N + h) cos(phi) cos(lambda) |
| Y | = | (N + h) cos(phi) sin(lambda) |
| Z | = | [N(1 - e2) + h] sin(phi) |
with:
The inverse conversion can be iteratively computed from:
| h | = | (X2 + Y2)1/2 / cos(phi) - N |
| tan(phi) | = | Z (X2 + Y2)-1/2 [1 - e2 N / (N + h)]-1 |
| tan(lambda) | = | Y / X |
В система Geomagnetic Coordinate system (MAG) ось Z параллельна оси магнитного диполя. Ось Y находится в одной меридиональной плоскости с географическими полюсами. Если D это положение диполя и S - южный полюс, то Y = D x S.
Географические координаты оси магнитного диполя, заданы International Geomagnetic Reference Field 1995 (IGRF-1995) как 79.30°N и 288.59°E для 1995 года. Величины для других эпох даны в Таб.2. Магнитный полюс движется со скоростью 2.6 км в год в направлении 15.6°N, 150.9°E. Подробнее в Fraser-Smith (1987).
| Year | Latitude | Longitude |
|---|---|---|
| 1945 1950 1955 1960 1965 1970 1975 1980 1985 1990 1995 |
78.47 78.47 78.46 78.51 78.53 78.59 78.69 78.81 78.97 79.13 79.30 |
291.47 291.15 290.84 290.53 290.15 289.82 289.53 289.24 289.10 288.89 288.59 |
Система GSE (The Geocentric Solar Ecliptic System) осью X направлена от Земли на Солнце, а Y расположена в плоскости эклиптики и направлена на вечер (противоволожно вращению планет). Соответственно ось Z параллельна -направлению на полюс эклиптики. По отношению к инерциальной системе эта система имеет годичный оборот вращения.
Система GSEQ (The Geocentric Solar Equatorial System) как и GSE имеет ось X направленную на Солнце, но ось Y лежит не в плоскости эклиптики, а в плоскости солнечного экватора, которая наклонена к эклиптике. -axis in the ecliptic plane, the GSEQ Y-axis is parallel to the Sun's equatorial plane which is inclined to the ecliptic. Поскольку ось X-лежит в плоскости эклиптики, ось Z этой системы не обязательно параллельна оси вращения Солнца, которая, однако, должна находиться в плоскости X-Z.
Система GSM (The Geocentric Solar Magnetospheric System), как и GSE и GSEQ имеет ось X направленную на Солнце. Ось Y перпендикулярна земному магнитному диполю так что плоскость X-Z включает ось диполя. Ноложительное направление оси Z - тоже к северному полюсу. Разница между GSM и GSE и GSEQ просто в повороте вокруг оси X.
В системе SM (Solar Magnetic Coordinates) ось Z направлена к северному магнитному полюсу, ф ось Y по нормали к линии Земля-Солнце на вечер Разница между этой системой и GSM во вращении вокруг оси Y на величину наклона диполя. В этой системе ось X не указывает прямо на Солнце. Также как GSM, SM вращается с суточным и годовым периодами по отношению к инерциальной системе координат.
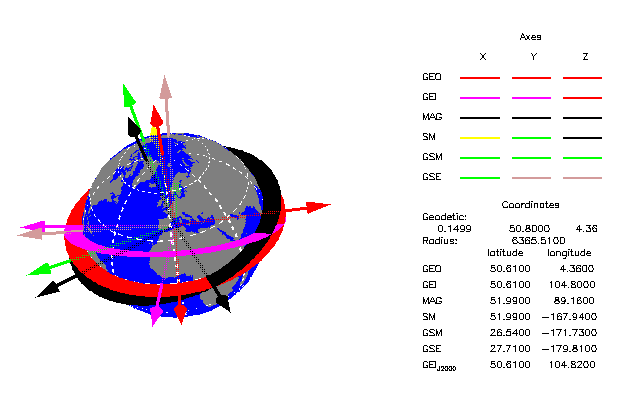 |
| Figure 3. Coordinate transformations for Brussels. The red ring is the geocentric equator, the black one the magnetic equator and the magenta ring is the ecliptic plane. |
| To | From | |||||
| GEI | GEO | GSE | GSM | SM | MAG | |
| GEI | 1 | T1-1 | T2-1 | T2-1T3-1 | T2-1T3-1T4-1 | T1-1T5-1 |
| GEO | T1 | 1 | T1T2-1 | T1T2-1T3-1 | T1T2-1T3-1T4-1 | T5-1 |
| GSE | T2 | T2T1-1 | 1 | T3-1 | T3-1T4-1 | T2T1-1T5-1 |
| GSM | T3T2 | T3T2T1-1 | T3 | 1 | T4-1 | T3T2T1-1T5-1 |
| SM | T4T3T2 | T4T3T2T1-1 | T4T3 | T4 | 1 | T4T3T2T1-1T5-1 |
| MAG | T5T1 | T5 | T5T1T2-1 | T5T1T2-1T3-1 | T5T1T2-1T3-1T4-1 | 1 |
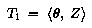
Эта матрица соответствует вращению в плоскости земного географического экватора от ервой точки Ариев к Гринвическому меридиану. Угол поворота theta есть гринвическое среднее сидерическое время, которое можно расчитать по формуле (U.S. Naval Observatory, 1989:
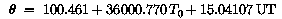
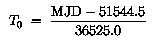
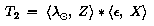
Это две матрицы соответствуют:
Эти два угла рассчитываются следующим образом. (U.S. Naval Observatory, 1989). Первый, epsilon, наклон эклиптики:
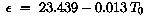
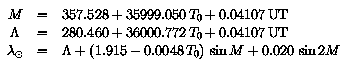
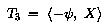
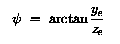
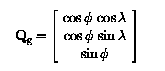
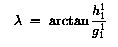
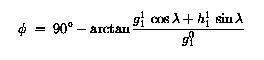
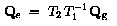
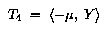

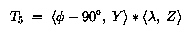
TУглы phi и lambda определены в секции T3.
Fraser-Smith, A. C., Centered and Eccentric Geomagnetic Dipoles and Their Poles, 1600-1985, Rev. Geophys., 25, pp. 1-16, 1987.
Goldstein, H., Classical Mechanics, Addison-Wesley Publ. Co., Inc., Reading Massachusetts, 1950.
Hapgood, M. A., Space physics coordinate transformations: A user guide, Planet. Space Sci., 40 (5), pp. 711-717, 1992.
Hapgood, M. A., Space physics coordinate transformations: the role of precession, Ann. Geophysicae, 13, pp. 713-716, 1995.
Hapgood, M. A., Corrigendum, Planet. Space Sci., 45 (8), pp. 1047, 1997.
Kelso, T. S., Orbital Coordinate Systems, Part III, Satellite Times, January/February 1996.
Magnetic and Electric Fields Branch, Coordinate Transformations Used in OGO Satellite Data Analysis, Goddard Space Flight Center Report, X-645-70-29, 1970.
Mead, G. D., J. Geophys. Res., 72 (11), 2737, 1970.
Olson, W. P., Coordinate Transformations Used in Magnetopheric Physics, McDonnell-Douglas Astronautics Company Paper WD1145, 1970.
Peddie, N. W., International Geomagnetic Reference Field : The Third Generation, J. Geomag. Geoelectr., 34, pp. 309-326, 1985.
Russell, C. T., Geophysical Coordinate Transformations, Cosmic Electrodynamics, 2 , pp. 184-196, 1971.
Smart, W, M., Text-Book On Spherical Astronomy, Fourth Edition, Cambridge Univ. Press, Cambridge, 1944.
U.S. Naval Observatory, Almanac for Computers 1990. Nautical Almanac Office, U.S. Naval Observatory, Washington, D.C., 1989.